Los De la Tarea: Número decimal

Para otros usos de este término, véase Decimal.

Este artículo trata sobre parte entera y parte fraccionaria. Para números escritos en base diez, véase Sistema de numeración decimal.

Se denominan números decimales aquellos que poseen una parte decimal, en oposición a los números enteros que carecen de ella.¹ Así, un número x perteneciente a R escrito usando la representación decimal tiene la siguiente expresión:

x = a, a_1a_2 \cdots a_n \cdots

donde a es un número entero cualquiera, llamado parte entera, separado por una coma o punto de la parte fraccionaria: cada a_i con i = 1,2,...,n,... y 0 ≤ a_i ≤ 9.² ³

3,1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989 3809525720 1065485863 2788659361 5338182796 8230301952 0353018529 6899577362 2599413891 2497217752 8347913151 5574857242 4541506959
Primeros 1100 decimales de π.

Índice

Parte entera y parte fraccionaria

La parte entera corresponde a un número entero (es decir que puede ser cero, o un número negativo); la parte decimal o fraccionaria, corresponde al valor decimal situado entre cero y uno.

Ejemplos:
- Logaritmo decimal, se distingue la mantisa de la característica; en log(0,001237) = - 2,90763 = -3 + 0,09237, la caractística es -3 y la mantisa es 0,09237.
- En base duodecimal, el desarrollo de √5 es 2,29BB13254051..., siendo 2 el entero y 29BB13254051... la parte fraccionaria.
- La notación científica permite escribir el número: 156 234 000 000 000 000 000 000 000 000 como 1,56234×10²⁹, siendo 1,56234 el coeficiente.
- La función parte entera es igual al mayor (o menor) entero contenido dentro de un número,

\lfloor 2,3 \rfloor = 2

\lfloor -2,3 \rfloor = -3

Notación decimal

Véase también: Separador decimal

Véase también: Separador de millares

En la lengua española en la actualidad se emplean básicamente tres formas de anotar un número con parte decimal, según el signo empleado como separador decimal:
El punto decimal: se emplea un punto(.) para separar la parte entera de la decimal, este método es el utilizado en las calculadoras electrónicas y en los ordenadores, rara vez se utiliza en la notación de cifras manualmente.

3.141592 \;

La coma decimal: se emplea una coma(,) como separador, esta forma en común en las publicaciones de habla hispana y se utiliza también en las notaciones manuales.

3,141592 \;

El apóstrofo decimal: el apóstrofo(') en ocasiones también llamado coma decimal es la forma usual de separar la parte decimal de un número en las notaciones a mano.

3'141592 \;

En todos los casos, las cifras decimales, no se separan en grupos con espacios en blanco u otro signo, sino que se escriben seguidas, sea cual sea el número de cifras decimales que forme la parte decimal del número en cuestión.

Cifras decimales

\begin{array}{lcccl} \hline \rm d\acute{e}cima & \longmapsto & 10^{-1} & = & 0,1 \\ \rm cent\acute{e}sima & \longmapsto & 10^{-2} & = & 0,01 \\ \rm mil\acute{e}sima & \longmapsto & 10^{-3} & = & 0,001 \\ \rm diezmil\acute{e}sima & \longmapsto & 10^{-4} & = & 0,0001 \\ \rm cienmil\acute{e}sima & \longmapsto & 10^{-5} & = & 0,00001 \\ \rm millon\acute{e}sima & \longmapsto & 10^{-6} & = & 0,000001 \\ \hline \end{array}

Aproximación decimal

Si se toman en cuenta las cifras significativas, el número 0.080 es distinto del número 0.08, pues aunque representan la misma cantidad, el primero indica un grado de aproximación con tres cifras decimales.

Fracción decimal

Véase también: Fracción decimal

Un número decimal

x = a, a_1a_2 \cdots a_n \cdots

admite una escritura formal (llamada la representación decimal) en base a series infinitas de fracciones decimales. Las fracciones decimales suelen expresarse sin denominador, con uso del separador decimal, es decir, como número decimal exacto.
Ejemplos:

8/10, 83/100, 83/1000 y 8/10000 se escriben 0.8, 0.83, 0.083 y 0.0083
en general: $\frac{N}{10^n}$ es una fracción decimal, en donde N es un número entero.

Representación decimal

Artículo principal: Representación decimal

Una fracción decimal no es necesariamente irreducible, pero todo número decimal finito puede escribirse como una fracción irreducible de la forma:

\frac{b}{5^m \times 2^p}

con b un entero primo relativo con 5 y 2, y m y p enteros naturales.
La representación decimal de los números reales (y por tanto de los racionales) se basa en el límite de series del tipo

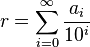r=\sum_{i=0}^\infty \frac{a_i}{10^i}

No unicidad en la representación decimal

La escritura decimal de los números reales no es única, se puede demostrar que 0,999...=1.⁴

Véase también: 0,9 periódico

La escritura de los números enteros (excepto el 0) y de los números decimales exactos no es única si se admiten secuencias recurrentes de 9.

Ejemplos:
- $1 = 1,\underline{0}... = 0,\underline{9}... = 0,99999...$
- $\frac{1}{2} = 0,5 = 0,499999...$
- El número cero (0) no tiene una representación con 9 recurrente.

Clasificación

Atendiendo a la definición, y llamando parte entera a la parte a la izquierda del separador decimal y parte decimal a la parte derecha del separador decimal, se puede construir la siguiente clasificación:⁵

\rm n \acute{u} mero \left \{ \begin{array}{l} \rm entero \\ \rm decimal \left \{ \begin{array}{l} \rm exacto \\ \rm peri \acute{o} dico \left \{ \begin{array}{l} \rm puro \\ \rm mixto \end{array} \right . \\ \rm no \ peri \acute{o} dico \end{array} \right . \end{array} \right .

Número decimal exacto

Los números decimales cuya parte decimal tiene un número finito de cifras se denominan números decimales exactos. Se pueden escribir como fracción, y por tanto, pertenecen a un subconjunto de los números racionales.

Ejemplos:
- $\frac{117}{20} = 5,85$
- $\frac 8 5 = 1,6 = \frac {16} {10}$

Estos números tienen la particularidad de que su representación decimal no es única. Así, por ejemplo, el número racional ¹/₅ se puede representar mediante el número decimal exacto 0,2 o mediante el número decimal periódico 0,1999..., luego ¹/₅ = 0,2 = 0,1999...

Número decimal periódico

Artículo principal: Número periódico

Son los números decimales cuya parte decimal tiene un número infinito de cifras que se repiten siguiendo un patrón, llamado periodo. Si el patrón comienza inmediatamente después del separador decimal, se denominan números decimales periódicos puros; si el patrón comienza después del anteperíodo, se denominan números decimales periódicos mixtos. Estos números también pertenecen a un subconjunto de los números racionales, puesto que puede ser expresados en forma de fracción.

Decimal periódico puro

Son los números decimales en los que la parte decimal se repite periódicamente, inmediatamente después del separador decimal. La parte periódica se suele señalar usualmente con una línea horizontal superior. Por ejemplo:

0,33333... = 0,\overline{3} \; =\frac{1}{3} =\lim_{x\rightarrow +\infty} \left( \sum_{n=1}^{x} \frac{3}{10^n} \right)

Decimal periódico mixto

Son los números decimales en cuya parte decimal hay una parte no periódica, denominada antiperiodo, y otra periódica. La parte periódica se suele señalar con una línea horizontal superior. Por ejemplo:

0,16666... = 0,1\overline{6} \;

Al igual que los números decimales periódicos puros, los números decimales mixtos siempre pueden ser expresados en forma de fracción; en el caso del ejemplo, la fracción equivalente sería ¹/₆.

Número decimal no periódico

Los números decimales no periódicos son los que contienen una parte decimal infinita y que no se repite. Estos números corresponden al conjunto de los números irracionales, y no pueden ser representados por medio de una fracción.
Algunos de ellos son:

\pi \, , \; e \, , \; \sqrt{2} \, , \; \sqrt{3} \, , \; \dots

Puesto que los irracionales contienen infinitas cifras decimales y ningún período, es usual expresarlos en forma simbólica. Para efectuar cálculos numéricos, se toma el valor decimal numérico con el suficiente número de cifras decimales significativas para la obtención de datos con una determinada precisión, ya sea redondeando o truncando.
Por ejemplo, en el caso del número π, aplicando un truncado a sus primeras cifras, se obtiene:

\pi \approx 3{,}14159265358979323846

Sistema de numeración decimal posicional

En el sistema de numeración decimal (de manera general, en un sistema de numeración posicional de base racional), las fracciones irreducibles cuyo denominador contenga factores primos distintos de los que factorizan la base diez (es decir, 2 y 5), carecerán de representación finita, dándose recurrencia pura cuando no haya ningún factor primo en común con la base, y recurrencia mixta cuando haya al menos un factor primo en común con la base.

Ejemplos:
- $\frac{15}{5} = 3$ Número entero
- $\frac{1}{2} = 0,5$ Decimal exacto.
- $\frac{1}{3} = 0,\overset{\frown}{3}$ Periódico puro.
- $\frac{7}{6} = 1,1\overset{\frown}{6}$ Periódico mixto.

Véase también

Clasificación de números

Complejos

\mathbb{C}

Reales

\mathbb{R}

Racionales

\mathbb{Q}

Enteros

\mathbb{Z}

Naturales

\mathbb{N}

1: uno

0: Cero

Irracionales algebraicos

Trascendentes

Imaginarios

Referencias

Número decimal
Jarauta Bragulat, Eusebi (2000). «1.4. Representación decimal de los números reales». Análisis matemático de una variable: fundamentos y aplicaciones. Barcelona: Editions UPC. pp. 20–23. ISBN 8483014106.
Ortega, Joaquín M. (1993). «1.3. Expresión decimal de los números reales». Introducción al análisis matemático (1ª edición). Barcelona: Editorial Labor. pp. 33–37. ISBN 843353047X.
Clapham, Christopher (1998). Diccionario de matemáticas / Diccionarios Oxford-Complutense (1ª edición). Madrid: Editorial Complutense. pp. 85–86. ISBN 8489784566.
Equipo Editex, ed. (2009). «1.6. Los números decimales». Formación básica. Ámbito científico-tecnológico. Madrid: Editex. pp. 22–23. ISBN 8497715586.

Los De la Tarea

lunes, 22 de septiembre de 2014

Número decimal